Teil 9: Warum logische Strukturen in Graphdatenbanken mit Edges besser abgebildet werden können

Bisher habe ich dir gezeigt, wie Fragen und Antwortmöglichkeiten eins Chatbots in einem Graph miteinander verbunden sind und wie darin Logik implementiert werden kann. Ein Chatbot ist nämlich das ideale Beispiel für komplexe vernetzte Strukturen.

Ich habe außerdem Graph Traversal zur Veranschaulichung mit einem Wanderer verglichen, der den Graph auf Straßen (Edges) und Kreuzungen (Nodes) durchquert. Im letzten Artikel habe ich die Logik vom Expertenwissen isoliert, um mehr Übersicht über den Graph und seine logischen Strukturen zu bekommen.

In diesem Artikel möchte ich dir erklären warum es sinnvoll ist, die Logik nicht mit Nodes, sondern stattdessen mit Edges zu beschreiben.

Logik in Knoten

Du erkennst auf der nächsten Grafik 2 verschiedene logische Tore in Gelb. Bei dem linken Tor handelt es sich um ein OR-Gate. Hier ist es egal, aus welcher Richtung der Wanderer auf das Tor trifft. Er kann in jedem Fall der ausgehenden Route folgen und die nächste Frage entdecken. Bei dem rechten Tor, dem UND-Tor, müssen zunächst alle eingehenden Wege benutzt worden sein, um zur nächsten Frage gelangen zu können. Dieses Konzept habe ich bereits in dem vorherigen Artikel beschrieben.

Logik in Edges

Sie dir die nächste Grafik an. Auf ihr erkennst du die gleiche logische Struktur, jedoch habe ich hier die Logik in die Edges ausgelagert:

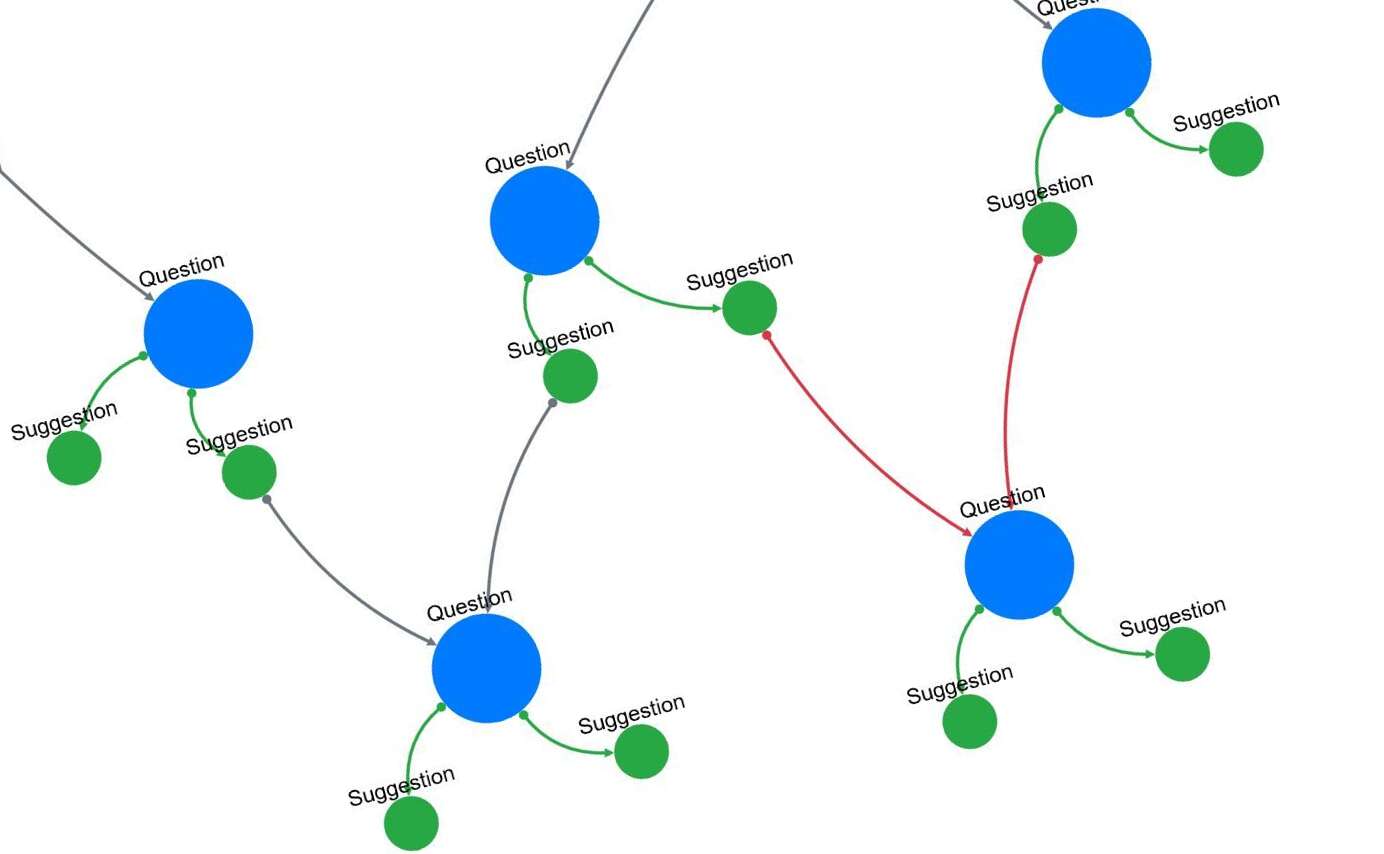
In diesem Konzept werden die logischen Knoten nicht länger benötigt. Die Logik steckt hier direkt in den Edges. Trifft der Traversal Prozess hier auf eine Frage, schaut er sich zunächst die eingehenden Edges an. Im linken Beispiel wird er 2 eingehende ODER-Edges (grau) finden. Da diese keiner genaueren Prüfung bedürfen, darf die betreffende Frage einfach gestellt werden.

Im Fall des rechten Beispiels hat die Frage jedoch zwei eingehende UND-Edges (in Rot hervorgehoben). Der Wanderer muss, wenn er auf diese Frage trifft hier zunächst prüfen, ob beide UND-Edges schon mal durchquert wurden. Die Information, ob es sich bei der Frage um eine UND- bzw. ODER-Prüfung handelt, wird allein durch die Edges festgelegt.

Warum ist das jetzt besser?

Die logischen Knoten müssen nicht immer mit eingebaut werden. Bei einfachen Prüfungen reichen so die eingehenden Edges aus. Durch weniger Knoten entsteht so ein besserer Überblick über den Graph und damit auch über die Strukturen der möglichen Konversationsverläufe.

Trotzdem können weiterhin Knoten eingebaut werden, die als Sammelstelle dienen, wenn mehrere Aktionen von denselben Bedingungen abhängig sind:

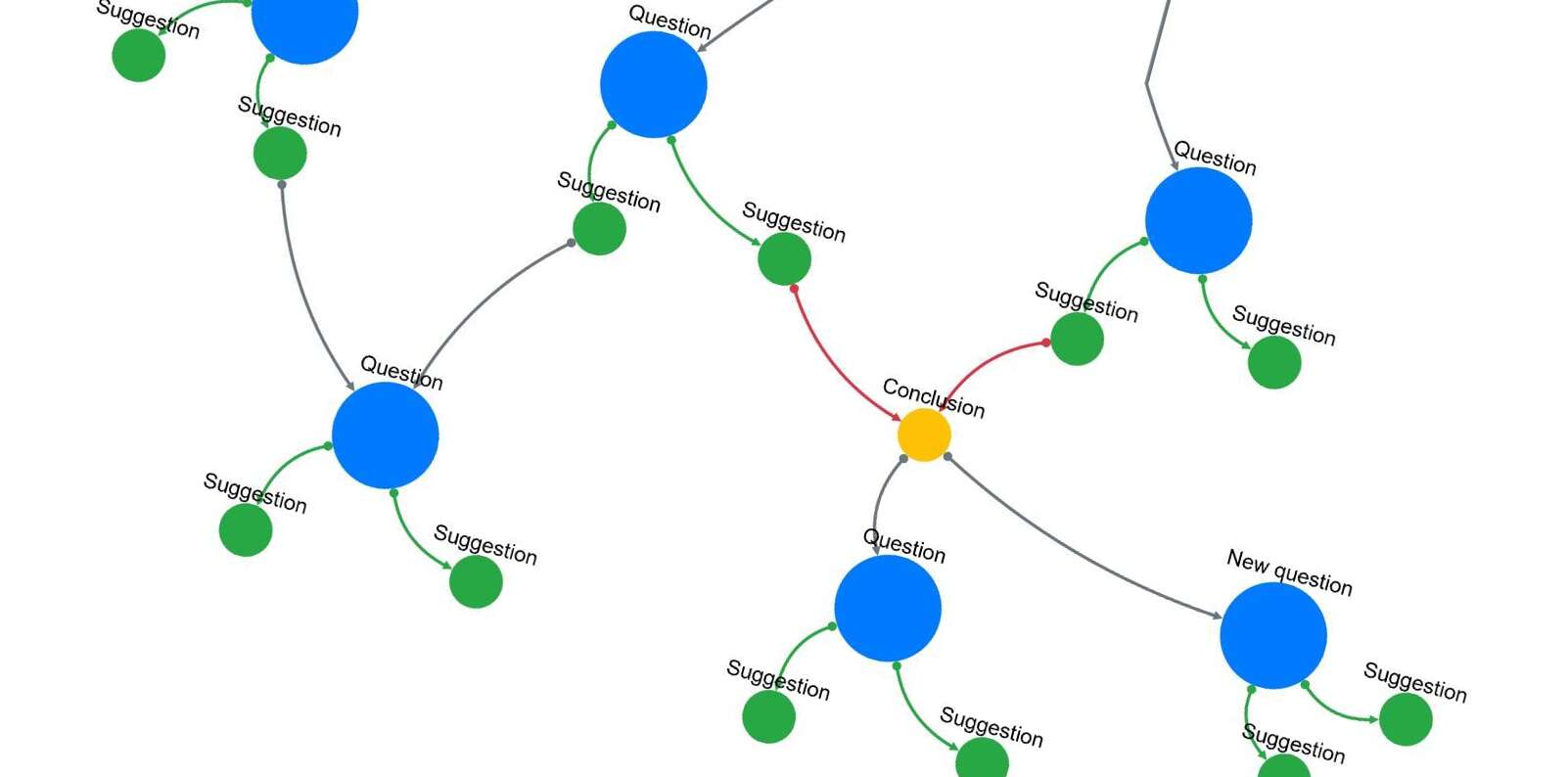
Auch wenn der gelbe Knoten weder explizit ein OR noch ein AND Knoten ist, wird der Wanderer zwei eingehende UND-Edges entdecken und diese prüfen, bevor die zwei Fragen darunter gestellt werden. Man könnte auch sagen, dass es sich bei diesen Sammelknoten um eine Art Schlussfolgerung handelt, auf denen wiederum weitere Aktionen basieren.

Es entstehen komplexe Gatter

Ein weiterer wichtiger Grund für dieses Vorgehen wird im nächsten Artikel deutlich. Denn es gibt noch mehr logische Funktionen als nur UND bzw. ODER. In einem Graph ist auch NOT, also eine Negation in Kombination mit UND bzw. ODER denkbar. Diese lässt sich allerdings nicht mit NOT-Knoten umsetzen, sondern nur mithilfe von Edges. Auf diese Weise ist es möglich durch verschiedene Edges komplexe logische Tore zu erschaffen.